Retour à la liste

Schematischer Beitrag zur Konvergenz-Blick-Geometrie

3 584 9

Albrecht Klöckner

Premium (World)

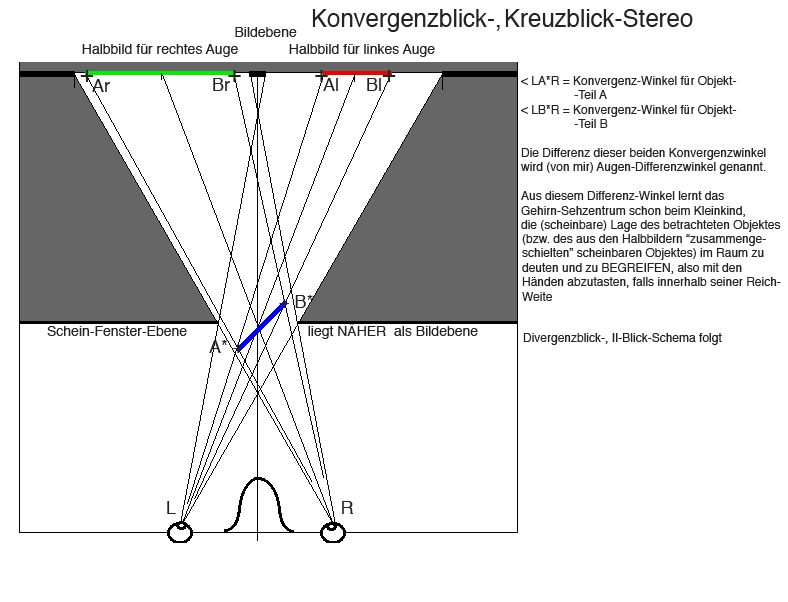
Schematischer Beitrag zur Konvergenz-Blick-Geometrie

Dies ist zwar kein Stereofoto, sondern soll zur Begriffs-Diskussion beitragen. Wie der Begriff "Deviation" hier hineinpasst, habe ich mir noch nicht erschlossen...
Entsprechendes Schema für Divergenzblick und Anaglyphe ist in Arbeit
Bin gespannt auf Kommentare AK

Commentaire 9

Silke Haaf 29/11/2005 5:38
http://de.wikipedia.org/wiki/Deviation_%28Stereografie%29

http://de.wikipedia.org/wiki/Diskussion:Deviation_%28Stereografie%29

P.s.: Die Zeichnung sehe ich mir demnächst mal ganz in Ruhe an, Albrecht...;-)
Faire l'éloge d'un commentaire
Michael K0ch 15/11/2005 8:07
Alexander, wenn man weiss, dass in der FC und nicht nur hier die SF-Ebene und die Bildebene häufig fälschlicherweise synonym verwendet werden, sollte man doch gerade dann darauf achten, die Begriffe korrekt zu verwenden, zumal unter einer Schemazeichnung, wo es doch gerade um die Bezeichnungen und nicht um ein Raumbild geht. Willst Du den Irrtum weiter verbreiten? Warum soll die FC kein Ort sein, wo terminologisch korrekt diskutiert wird? Jemanden, der die Begriffe noch nicht kennt lehrst Du damit etwas Falsches bzw. erschwerst Du das Verständnis.

Gruß, Michael
Faire l'éloge d'un commentaire
Alexander Kriegisch 13/11/2005 17:11
Michael, Du hast ziemlich viel wiederholt von dem, was ich bereits in kürzerer Form geschrieben hatte. Daß ich vulgo für alle Raumbildtypen den Begriff Scheinfensterebene synonym zu Bildebene benutzt habe, liegt daran, daß das zwar nicht terminologisch korrekt ist (ich weiß!), aber im FC-Sprachgebrauch eben häufig so benutzt wird. Ich glaube, es haben auch alle richtig verstanden. Deine Klarstellung ist dennoch sachlich richtig somit nützlich.
Faire l'éloge d'un commentaire
Michael K0ch 13/11/2005 13:27
Ja, gutes Schema, Albrecht!

Alexander, die Deviation - besser der Versatz - korrespondierender Punkte der Halbbilder hat *nichts* mit ihrer Lage zum Scheinfenster zu tun, sondern mit ihrer Lage zur Bildebene.

Fallen korrespondierende Punkte der Halbbilder auf der Bildebene zusammen, liegt der resultierende Raumbildpunkt genau in der Bildebene (Beispiel: ein gewöhnliches 2D-Bild als flache Anaglyphe interpretiert). Ist die Reihenfolge der korrespondierenden Punkte von links nach rechts gesehen "Punkt des Halbbildes für das linke Auge" "Punkt des Halbbildes für das rechte Auge" liegt der Raumbildpunkt hinter der Bildebene, ansonsten vor der Bildebene. Dies gilt sowohl für Anaglyphen als auch für nebeneinander montierte Halbbilder für Parallel- oder Kreuzblick. Beim Parallelblick ist die Reihenfolge immer "links rechts", beim Kreuzblick immer "rechts links" und bei gewöhnlich montierten Anaglyphen (ebenes Scheinfenster in der Bildebene) "links rechts", bei Scheinfensterdurchbrüchen "rechts links".

Fernpunktversatz: Der Maximalwert der Differenzen der x-Koordinaten aller korrespondierender Punkte der Halbbilder, und zwar x-Koordinate des Punktes im rechten Halbbild minus x-Koordinate des Punktes im linken Halbbild (bei Kreuzblickmontagen der positivste negative Wert)

Nahpunktversatz: Der Minimalwert der Differenzen der x-Koordinaten aller korrespondierender Punkte der Halbbilder, und zwar x-Koordinate des Punktes im rechten Halbbild minus x-Koordinate des Punktes im linken Halbbild (bei gewöhnlich montierten Anaglyphen mit Scheinfensterdurchbruch leicht negativ)

absolute (Bild-)Deviation: Die Differenz von Fernpunkt- und Nahpunktversatz (in Pixeln oder Millimeter)

normierte (Bild-)Deviation: Der Quotient von absoluter Deviation und Bildbreite (z.B. in % oder ‰)

Bei nebeneinander montierten Halbbildern ist der Betrag des Nah- und des Fernpunktversatzes gegenüber sich deckend montierten Halbbildern um die Halbbildbreite und die Mittelstegbreite extrem vergrößert, das Raumbild befindet sich daher im Vergleich zu Anaglyphen weit vor (Kreuzblick) oder weit hinter (Parallelblick) der Bildschirmebene. Aufgrund dessen muss man diese Raumbildmontagen mit besonderen Blicktechniken betrachten. Mit normalem Blick hat man dabei sozusagen überall Bildzerfall aufgrund des riesigen Fern- und Nahpunktversatzes.

Der Fernpunktversatz ist genau dann die Deviation des Raumbildes, wenn der Nahpunkt in der Bildschirmebene liegt. Die auf die Bildbreite normierte Deviation eines Raumbildes kann maximal 200% betragen.

Die Deviation ist im Unterschied zum Augen-Differenzwinkel unabhängig vom Augen- und Betrachtungsabstand.

Gruß, Michael

Deviation: http://www.herbig-3d.de/german/stereobasis.htm#5

[Beitrag editiert am 27.10.2012]

Maximale Tiefe
Michael K0ch

Faire l'éloge d'un commentaire
Ralf Fackiner 12/11/2005 15:37
Vielen Dank für diese Arbeit, Albrecht!
Freut mich immer, hier etwas zu Grundlagen zu finden.

Jetzt sollte noch ein passendes Bildbeispiel dazu, evtl. mit verschiebbaren Objekten. Oder einfacher eine Bildfolge, damit es jede/r laden und betrachten kann.

Viele Grüße von Ralf
Faire l'éloge d'un commentaire
De Wolli 08/11/2005 17:19
Wichtig ist, wie du schon sagst, das Alter, also die Akkomodationsfähigkeit des Probanden in dem Zusammenhang. Ebenso das Fusionsvermögen.
Junge Menschen können durchaus auf einen Punkt in der Nähe der Nasenspitze akkomodieren (scharf stellen) ältere sind oft froh, wenn sie noch ihre Füße sehen (kleiner Scherz). In Nasenspitzennähe ist natürlich der Augeninnenmuskel enorm beansprucht, das hält man nicht allzu lange aus, ohne Kopfschmerzen zu kriegen.
Hier dürften konvergenzentlastende Prismen ganz gut funktionieren, allerdings kosten Spezialbrillen, die sowas können, ab 250 Euro aufwärts. Teurer Spaß, nicht?
Schöne Erklärung von Alexander übrigens.
Faire l'éloge d'un commentaire
Albrecht Klöckner 08/11/2005 17:10
Danke, Wolfgang und Alexander. Dann hat also "Deviation" direkt mit meinem "Augen-Differenz-Winkel" zu tun. Fürs Erste ziehe ich meinen Begriff vor, bin allerdings gespannt, wie der sich in Divergenz-Blick-Stereos und Anaglyphen bewährt, das muss ich in Schemazeichnungen noch genauer herausfinden.
Eine interessante Frage in diesem Zusammenhang ist dann auch, wer sich wieviel Deviation bzw. Differenzwinkel eingeübt hat.
Mein Maximal-Divergenz-Winkel ist so ca. -4° (also nach außen schielend), nach innen komme ich bis auf ca. +80° Konvergenz-Winkel, also fast bis zum "Anschlag Nasenrücken", so nahe OBJEKTE bekomme ich allerdings ohne "Nahlinsen" nicht mehr fokussiert. Bild-Zerfall tritt besonders leicht auf, wenn zwischen Nächst-Punkt und Fernst-Punkt keine "optischen Trittsteine" sind , über die man "mit den Augen schrittweise in die Bildtiefe gehen" kann, wenn also zwischen Vordergrund und Hintergrund nicht genügend oder gar kein Mittelgrund angeboten wird.
Spannendes Thema!
Gruß
Albrecht
Faire l'éloge d'un commentaire
Alexander Kriegisch 08/11/2005 16:21
(Achtung, ich labere jetzt Zeug daher, das viele sowieso schon wissen. Soll keine Belehrung sein, ich bin ja selber nur ein besserer Anfänger. Vielleicht regt es aber trotzdem die Diskussion an.)

Nun, die Deviation, also der horizontale Abstand (in Px oder Prozent der Bildbreite) zwischen korrespondierenden Punkten beider Halbbilder, also z.B. Ar-Al oder Br-Bl, bestimmt ja, ob der resultierende räumliche Bildpunkt vor oder hinter der SF-Ebene liegt. Dabei ist natürlich nicht nur der Betrag, sondern auch das Vorzeichen der Deviation maßgebend. Ist sie null, liegt der Punkt bekanntlich in der SF-Ebene. Bei "klassisch" gerahmten Bildern hat die Deviation aller Bildpunkte das gleiche Vorzeichen (alle Bildpunkte hinter dem SF). Bei "Effekt-Stereos" sieht das anders aus, denn da gucken ja auch Bildpunkte aus der SF-Ebene heraus, haben also eine negative Deviation, wenn wir mal festlegen, daß hinter der SF-Ebene liegende Punkte eine positive Deviation haben sollen.

Die absolute Bild-Deviation, also die Differenz zwischen Nahpunkt-Dev. und Fernpunkt-Dev., ist nicht nur ein Maß für die gesamte räumliche Tiefe des Bildes, sondern auch ein Maß dafür, wie schwierig es ist, das Bild zusammenhängend (ohne Bildzerfall) zu betrachten.
Faire l'éloge d'un commentaire
De Wolli 08/11/2005 15:43
Da hast du dir ja richtig viel Mühe gemacht. So kann man es eigentlich sehr schön verstehen.
LG
Wolfgang
Faire l'éloge d'un commentaire